（１）「知っている事は必要条件にすぎない！」
―教師が持つべき最も優先順位の高い能力は実践的授業スキルである。“知っていること”はそのスキルの要素にすぎないー
「教職大学院」や「教職免許更新制」等の動きは、つまるところ現場の『実践的授業スキル』を強化しようという動きと考えられます。では何故これまでこの最も重要な分野が放置されてきたのでしょうか。次の理由が考えられます。
（ｲ）「知っていれば教えられる」そこから先の『実践的授業スキル』は個人的努力で少しずつ経験的に積み上げていけばよいという共通認識があったこと。
（ﾛ）『実践的授業スキル』が系統化、標準化しにくいと考えられていること。
（ｲ）の「知っていれば教えられる」という迷信はいまだに根強い影響力をもっています。
「教育」とは教えることであり、「教師」は教える人である。その際現状では「知っていること」以外に教師のもつべき必要条件については共通のイメージがないのが現状と考えられます。建て前はともかく実質上、授業現場での主体（主人公）は教師であり、生徒は教えられる受身的存在と位置づけられています。教師は知の体現者であり、子供に知を切り売りするという構図です。この構図では、教師側については知の体現者として十分な知識を有しているかどうかが最も重要な要素ということになります。家庭のお父さんやお母さんが有名大学の学生さんに家庭教師として我が子を託せるのは将に「知っていれば教えられる」と考えるからでしょう。
そもそも授業の主要な構成要素は生徒と教師そして授業内容としての知の３つと考えられます。そして教師が生徒への「知の媒介者」であるとすれば、教師は生徒の持っている回路とかみ合う形でしかも効率的に（速く、印象深く・・）知を提供しなければならないはずです。即ち教師は授業内容と関連のある既習内容の生徒への定着度合いを素早く探り、イメージ化しやすい形に加工した知を、生徒の回路への定着具合を質問によって確認しながら授業を進めなければならないはずです。
新人教師が生徒の状況にお構いなしに一方的にしゃべりまくったり、生徒のつまずいてるありかがわからずに、本来一言で納得させられる場面でくどくどと空回りのの説明をしている姿を何度も見てきました。このように「知っていれば教えられる」というのは大いなる幻想なのです。

（２）「教師は知の生徒への媒介者である！」
一問題解決主体を本気で生徒と位置づければ、教師の本質的役割は知の媒介者である。知の媒介者の最も優先順位の高い能力は、生徒の自己回路と「知」を切り結ぶ『実践的授業スキル』である一

授業が生徒の力を高めるためにあることを考えれば、授業の主人公が生徒である事は明らかであり、これを否定する教師もいないでしょう。問題はここから先です。「生徒を問題解決主体とする授業方法」はあるのか、それは何なのかということです。
生徒を問題解決主体とする授業とは、生徒の既存の回路（思考回路、感性回路、経験知など）を授業展開の中枢に据えるということです。現在の多くの授業は教師の内にある知のあり方や思考回路に生徒をつき合わせる教師主体の授業になっています。そこでは教師のあらかじめ考えている説明や解法が正解であり、そこからはずれるものは排除されるべきノイズということになります。誤りは基本的にはノイズとして切り捨てられるのです。誤答した生徒は、教師の考えている「正解」に自らの回路をつながなければならず、失敗すれば「落ちこぼれる」ことになるわけです。
生徒の回路（本書では自己回路と呼ぶ）が最も重視されるべき授業要素だとすれば、教師の役割は質的にかわってきます。即ち教師に主要に求められるのは、知の体現者としての能力（＝授業内容に精通している）ではなく「知の媒介者」としての能力ということになります。
「知の媒介者」であるためには「知に精通している」事は勿論、「生徒の自己回路を徹底して重視する実践的授業スキル」をもっていなければなりません。知っている事は教師としての要件の必要条件ではありますが、必要十分条件ではないのです。有名大学出身の親や、学生がまともに教えられないのはこのスキルが身についていないからと考えられます。「いや、うちの学生家庭教師はよく教えている。子供もなついている」というお父さん、お母さんもおられると思います。授業風景を１５分見学させてもらってください。「これはこういう風に解くんだよ。覚えてね。」という教師の回路に生徒をつき合わせる方式になっていませんか。

授業の性質　　　　　　求められる能力
教師主体の授業　⇒　・授業内容を知っていること
生徒主体の授業　⇒　・授業内容を知っていること
　　　　　　　　　　・生徒の回路と知を切り結ぶ授業スキル

II　「問答法授業って何？」

（１）「生徒（主体の授業は歴史的要請である！」
生徒の自己回路を重視する（生徒を主人公とする）授業は、従来も建て前としてはその必要性は認められてきました。授業において生徒が重要だということは、当然どの教師も認めるところです。問題は、実際の授業が生徒の回路を中心とした授業の組み立てか、教師の回路を中心とした授業の組み立てかということです。
私達は現在「高度情報化社会」（「ソフト化社会」「知識社会」）の到来という歴史的転換点に直面しており、その結果、社会的に有用な能力の中核が「より多く、より速く、より正確に」から「広義の創造力（発想力）」及びその能力の前提となる「情報判断力（情報駆使能力）」へと変化しつつあります。その「広義の創造力（発想力）」や「情報駆使能力」は、既存の知のあり方を外から受身的にそのまま受け入れる能力ではなく、自分の固有の回路（自己回路）をどのように使いこなせるかという能力の強化と密接に結びついていると考えられます。広義の創造力も「無から何か有用なものをうみだす能力」ではないはずです。自分の内にある既存の情報系を駆使し尽くした先に、創造の世界が見えてくるわけです。従って「生徒の自己回路を重視する授業」という命題は、教育の建て前ですむ状況ではなく、生徒が社会にでて「食べていく」ための能力育成として本気で取り組むべき教育課題となっているわけです。では生徒の自己回路を重視する授業はどのようにして可能でしょうか。
育成すべき能力と授業方法との対応
・「より多く、より速く、より正確に」

　―　結果としての知の定着が重要　―　教師の一方的授業

・「広義の創造力、情報駆使能力」

　―知の定着のプロセス（情報駆使プロセス）が重要　―　生徒の回路中心の授業

（２）「問答法って何？」
生徒の自己回路を中核要素とする授業とは、単純化すれば授業内容（知）が生徒の自己回路にくみこまれるということです。生徒の自己回路は極めて多様であり、問題集や参考書で想定しているものはその中のごく典型的なものを考慮しているにすぎません。学習書やテレビ講座等は教師の一方的授業を徹底した学習様式といえるでしょう。このような一方通行の教師主体授業で生徒が十分に理解するのであれば、大半の教師は必要がないということになります。一方通行の授業では、生徒は提供される知を、自ら自己回路にくみこまなければなりません。これに失敗すれば落ちこぼれることになります。逆に自らくみこむことのできる生徒にとっては教師は必要ないわけです。したがって生徒の回路との切り結びの（ｽｷﾙの）ない授業は、生の教師が教壇に立つ根本的意義を失った失敗授業といえるでしょう。
（注）問題集の解説に自己の回路を切り結ぶことのできるような生徒は教師なしで自主学習できるわけですが、それでも教師は必要です。第一に効率の面でポイントを押さえた「これだけ」という授業は定着効率を飛躍的に高めます。第二にかなり理解力のある生徒でも、取り組む問題も高度化するので理解しにくい問題は存在します。私の経験でも、ほとんど学年トップであった生徒が、毎回問題集の間違い箇所に印をつけて質問していました。このように、力のある生徒でも自分だけでの取りくみは多くの場合不完全なものであり、時間の経過と共に行き詰まりがはっきりしてくる場合が多いようです。

生徒の自己回路情報を確認しながらその回路に知をくみこむ授業は、生徒の自己回路との対話としての「質問形式」で行われることとなります。「今の担任の先生も質問が多く、なるべく生徒に答えさせようとしている」と考えている保護者もおられるかもしれません。授業をよーくみていただきたい。質問は授業内容を生徒の回路にくみこむために行われているのか、教師の考える解法（回路）に生徒をつき合わせるために行われているのか。誤答の際に、その誤答した生徒の回路と解を切り結ぼうとしているのか、誤答回路は切り捨てて「他にわかる人？」という形で教師の想定する解に強引に誘導しようとしているのか。授業は生徒の回路中心か教師の回路中心かで中間はありえません。似て非なるものを上記の視点で見分けていただきたい。問答法においては、質問は単に「既にある情報を取りだす」ことだけが目的ではありません。質問により生徒の自己回路に知を形成、構築していきます。

質問の役割
・通常―教師の回路に着き合わせるための付録としての質問
・問答法―生徒の回路の中に知を築く作業そのもの

「問答法」とは生徒の思考回路に沿った質問の連続により、正答又は自己矛盾に導き、教師はそのプロセスに足跡を残さず、生徒の気づきを活性化させる触媒の役割に徹する授業方法です。そして生徒は自分だけでも解くことができたんだという形で終わることになります。生徒は問題解決の手がかりを教師によって与えられた瞬間に、自己回路の中にその手がかり（情報）をさがそうとする意欲を失ってしまいます。なぜなら既に問題解決に役立つ有用な手がかりや解そのものが与えられているからです。実質上解が与えられた場面では、その解や手がかりを受身的に受け入れる（≒覚える）ことが主要課題となります。
即ちここでは課題（問題）と自己の回路（経験知や既習事項等の既知情報）とをどう切り結ぶかという「問題解決のための情報駆使力」の訓練が行われないことになってしまいます。もう少し具体的にみてみると、生徒はPの位置におり正答はQの位置とします。生徒は角のA,B,Cでそれぞれ曲がる方向を考えなければなりません。例えばAにおいて直進か、左折か、右折かの判断力が必要となります。ここで教師が手を引いて右に導くのは、生徒の自己回路重視と言うことにはなりません。

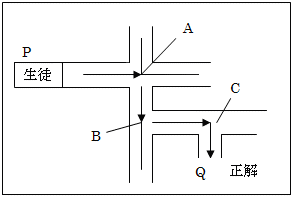
問答法では教師は、どちらを選択すべきかを考える際の考え方を質問により活性化させ、正解への判断を導くことになります。それはヒントを与えることではありません。

ヒントを与えればそれは教師の足跡を残すことになります。
教師は解の図柄を描いていきます。しかしその図柄は白紙のキャンバスに教師が描くのではなく、生徒の自己回路の内に生徒自身の内にある情報を用いて、質問を介して生徒自身に描かせるのです。生徒自身の内にある情報の、どれをどのように活用すべきかについても、潜在的には生徒自身が知っているのです。なぜならその情報駆使には論理的必然性があるからです。その論理的必然性への気ずきをｻﾎﾟｰﾄするのが問答法における教師の役割です。既にあるものを本人にみえるようにサポートするのが問答法における教師の役割ということになります。但しどちらに曲がるべきかを判断するための知識が欠如している場合は、その判断にその知識が必要だという事を本人に自覚させた上で、知識は供給されなければなりません。
「生徒がつまずいた時の教師の役割」
・ 通常―教師にとっての正解を生徒の回路の外側に示す
・ 問答法―生徒の誤答の回路と知を質問によって切り結び、本人に自分の回路のどこが間違えているか気づかせる。

（事例）適当な関係代名詞を入れよ。（導入は終了している場面。Thatは除かれている。）
I　know　the　boy　（　　）father　is　a　teacher.
（実況中継）A「新人教師」B「生徒」C「研修指導教師」
A「B君何が入るかわかるかな」
B「……」
A「先行詞のthe boyは人だよね」
C「生徒がどこでつまづいているかの情報を得るにはまず和訳ですよね。わからない単語があるかもしれませんし、関係代名詞の入った文の訳し方がわからなければthe boyが先行詞だということもわかりませんよね。」
A「B君日本語にしてみて」
B「私はお父さんが先生である少年を知っている」
A「いいね。先行詞はどれ」
B「the boy」
A「じゃー何格」
C「つまづいている人を対象とする場合は、部分は部分として決着をつけた方がいいですね。つまりこの場合関係代名詞の種類と格という二つの要素があるわけです。種類については先行詞がthe boyとわかったので決着がつきますよね。種類はwhoというところまで引きだして、じゃー何格使おうかというように到達場面を鮮明な形で確認してから次の段階にいった方がよいと思います。」
A「先行詞がthe boyで人だから関係代名詞の種類は何？」
C「何故“人だから”などと余計なヒントを与えるのですか。生徒は先行詞が何を基準に分類するか忘れているかもしれないじゃないですか。教師は生徒に外側から何かを教える存在という先入観がまだぬけ切らないのかもしれませんね。問答法では教師は生徒から解を引きだす役割です。」
A「つづけます。関係代名詞の種類は？」
B「who」
A「いいね。次は格だね。」
C「生徒自身は関係代名詞は種類と格がポイントであることを忘れているかもしれませんね。そうすると“次は格”だと教え、誘導することになりますね。」
A「格が課題になっていることをどうやって引き出すかちょっと思いつきません」
C「生徒にとって自然に問題意識がそちらに向くようにするには現在の到達段階を鮮明に示せばよいと思います。即ちwhoまでは到達しているわけですからwhoに格変化がありwho whose　 whomと三種類あってどれを使えばいいかという形で問題設定すればB君にとっても格に関心が向くことが自然だと感じると思いますよ。」
A「じゃーB君whoの格変化を言ってみて。」
B「who　 whose　 whom」
A「じゃーどれ使うの？」
B「……」
A「主格、所有格、目的格のどれを使うかはどうやって決まるの？」
C「格の決め方についてA先生自身どうお考えですか？」
A「関係詞以下の文の中での先行詞の役割、格で決定します。」
C「生徒にはそう言って欲しいんですか。少し抽象的ですよね。論理を身につけさせたい時は、生徒にとってわかりやすくシンプルで具体的なおぼえ方にまで加工する（知っている知を授業知へと加工）必要がありますよね。最も簡単に格を決めるには具体的にどうすればよいのでしょう。」
A「二つの文に分けるのでしょうか？」
C「実質上はそういう意味にもなりますが、具体的指示としては“先行詞を関係代名詞以下の文に日本語でいれる”ということだと思います。本来の論理からいっても正しいわけですし又２文を関係詞を使って結びつける時にもそのまま使えますよね。勿論関係詞の次が動詞ならば主格などというその場しのぎの教え方はしません。いわれてみればあたり前のようですが、これまでの研修でもそのようにして格の決定をした先生はほとんどおられないのです。」
A「じゃーB君。格の決定のやり方はどうするの？」
B「先行詞を関係代名詞以下に入れる。<実際は導入時に執ように強調されるので覚えている子もいるわけです>」
A「入れてみて。」
B「少年のお父さんは先生です」
A「“少年の”は何格？」
B「所有格」
A「じゃー関係代名詞は何格？」
B「所有格」
A「つまり？」
B「whose」
A「よし、よくできたね。じゃー次の問題。」
C「ここで先生によるポイントのまとめが必要ですね。誤答の場合どうしても部分に細分化してから全体を構成していくことになります。子供は目先の部分に集中して全体構成が忘れられる場合があります。ですから部分の確認に一定以上のエネルギーを使った場合は、最後に全体像を鮮明に描いて生徒と再確認する必要があります。ここは教師の出番です。生徒のなかに一応描かれた正解へのプロセスについて、そのポイントが何であったのかを意識化（再確認）させることは重要です。」
A「関係代名詞のポイントは二つだけだね。種類と格だね。先行詞が人ならwho、物や動物ならwhichだったね。格は先行詞を関係詞以下に日本語で入れると決まるんだったね。種類は先行詞をみるだけですぐわかるから結局最大のポイントは格を決定するために先行詞を日本語で入れられるかどうかということになるね。」
C「いいですね。じゃー終わります。」

III「問答法の成立条件は何か？」

（１）「授業で扱われる知は、生徒を主要素とする知へと加工、変容されなければならない」
授業で扱われる知が教師の中でどのような状態にあるかは、次の三つに分類できるでしょう。
a：関連する知を全て知っており問われれば答えられる状態。
b：関連する知を全て系統的に理解し、一応知自体の系統性に基づいて生徒の前で発信できる状態。
c：生徒の状態をふまえてbの知を変容、加工できるスキルを持っている状態。（ここでは授業で通用する知の状態として『授業知』と呼ぶ）
aとbまでは机上で一応こなすことができるでしょう。しかしcの段階は、一定の研修や経験を経て、初めて得られる知の様相と考えられます。授業知への授業内容の加工は商品開発で消費者（ここでは生徒）の状況に合った商品を開発する作業と似ている。性能が良く、一流デザイナーによるハイセンスな商品を開発しても、それはこちら側（供給者）の論理であり、向こう側（消費者）とかみ合うとは限らないわけです。授業においても消費者である生徒の状況をふまえた知（授業知）が供給されなければならないわけです。
（２）「授業で使える知（『授業知』）への加工、変容はこうやる！」
生徒を本気で授業の主人公とするためには、授業で扱われる知は生徒の状態を主要素とする知に変容、加工されなければなりません。知はそれ自体一定の系統性、秩序をもっており、それを理解していることは教師にとっての必要条件です。『授業知』としては更にそれらの変容、加工する「実践的授業スキル」が必要なのです。
ではどのように変容、加工すればよいのでしょうか。
a：「生徒の既知（学習面での既習知と経験知常識）のレベルを探りそれとリンクさせる事」
学校や塾での授業は常に既習内容を前提とするので、それらとリンクさせる事は当然と考えられているかもしれない。しかし（イ）既習内容であるから理解しているはずという立場と、（ロ）目の前の現実の生徒が新範囲理解に必要な既習内容をどの程度理解しているかを実際に探る作業をするという立場では授業の質が違ってきます。
（ﾛ）は新範囲説明において、単に関連する既習内容を教師が必要と判断する範囲でサラッと触れるということではありません。既習事項の消化の度合いを知るには「質問」によって目前の生徒の回路とﾘﾝｸする必要があります。生の生徒の状態を質問で把握することで本物の生徒の回路とのリンクが果せるわけです。生徒の既知情報についての状況把握が授業知形成の出発点となります。
b：「どこまでを一区切り（一幕）とするかを生徒の状況をふまえて判断する。」
英語において「現在完了」の用法やbe動詞の種類を一つずつ教えるか、まとめて教えるかの判断等は重要です。生徒の状態によって消化効率の最も高い区切り方があるはずです。
c：「右脳的処理、イメージ化を可能とする知の変容、加工」
印象深く、後に残る一まとまりのイメージとして知を描く工夫がなされていること。
（ 第 I 章四条を参照してください。）
d：「その場で一応理解、納得すればよい内容と覚える内容を峻別し、覚える内容は『ここだけ』と生徒が意識できるようにすること」
理解なしの「暗記」は定着、応用の観点から極力避けるべきである事は明らかです。問題はここから先です。理解すべき事と覚えるべき事の峻別、また覚える事のなかでも、その中核をなす部分と周辺説明（知識）の区別が、生徒にそれとわかるように提示されなければなりません。又その峻別も生徒の状況によって変わってくるわけです。このように知へのﾒﾘﾊﾘをつける作業は教師の重要な役割です。そのためには教師の中でその峻別された授業知が形成されていなくてはならないわけです。教師研修において、その教師がどのようにﾎﾟｲﾝﾄのしぼりこみを行うかを見ればその教師の大体の力がわかるものです。

・授業知の作り方
知の系統的理解－学習内容の理解の前提となる既習知の確認―対象に応じた量の確定―知の加工(右脳的処理、ここだけというしぼりこみ)
－

（３）「教師の発想の転換研修が必要！」
教師も白紙の状態で生徒の前に立つわけではありません。大半の教師は「教えるぞ！」という構えで生徒の前に立っているわけです。教師は教える立場、生徒は教えられる受身的立場というわけです。この教師の意識を、「教師の役割は生徒から解を『引き出す！』役割である」という意識に転換する必要があります。前者は問題解決主体が教師であり、後者は問題解決主体は生徒となります。
そして「引き出す」視点での授業は、教師に新たな課題の設定を迫ります。向う側の回路（生徒の回路）に深く入り込まなければ「知っている」だけでは「引き出す」授業は成立しません。ここで生徒の回路と授業で扱う知とをﾘﾝｸさせるスキルが必要となるわけです。「ｺﾍﾟﾙﾆｸｽ的転回」とも言うべき「問題解決主体の変換」を実現するｽｷﾙの習得には系統的研修が不可欠と考えられます。

・ 教師の資格
従来　―　知を系統的に知っていること
問答法　―　知を系統的に知っていること
　　　　―　生徒の回路と知を切り結ぶ授業スキルのあること⇒問題解決主体を教師から生徒に移す研修が必要

（４）「生徒が自己の回路を開放しやすい空気が漂っている事」
第一章の第七条でも触れましたが、問題解決主体を生徒に移し、生徒の回路中心に授業をくみたてるには、生徒自身が自己の回路を開放しやすい空気が漂っている必要があります。それは生徒が教師の質問に、たとえ自信がなくても、何とか答えよう、自分の考えを表現しようと思えるような空気です。やや見当はずれの答を嘲笑したり、「できる人」中心の授業であったり、又逆に進んだ子が退屈するような、そんな空気では、生徒は積極的に自己の回路を開放せず、効果的に問答法を駆使できません。
しかしこのような「開放的空気」は既にあるものではなく、教師が意識的につくりださなければなりません。「他者を傷つける言動は許さない」という一貫した授業姿勢と、わからない人と退屈な人をださない綱わたり授業を行おうという教師の迫力が、少しづつそのような“自己開放しやすい空気”をつくっていくわけです。

・ 教室の空気
通常―教師がまともに知を発信できる雰囲気(「おしゃべりがない、集中して聞いている」等)
問答法―たとえ不十分でも生徒が情報発信しやすい雰囲気

IV「 問答法における教師の役割は何か？」

（１）「教師は黒子である！」
問答法授業では教師は（新しい範囲の説明場面を除けば）「黒子」であり、表舞台の主人公は生徒です。授業では教師による質問の連続で生徒がどんどんあてられ、生徒は息を抜けません。質問内容（答ではない）を聞いていなかった場合、緊張感を維持するため次回指されるまで立って授業を受ける約束になっています。廊下ではなく、授業の場で生徒を立たせるのは体罰ではありません。教師と生徒には「授業内容がわからないのは教師の責任、問題内容を聞いていないのは生徒の責任」との確認があるのです。問答法授業は答や関連する知を「教える授業」ではなく「引き出す授業」なので「問題解決主体」は生徒ということになります。教師は黒子の役割であり、表舞台に足跡を残さない授業が成功した授業ということになります。
具体的に数学の練習問題の場面などでは、まずその答を導くのに必要な条件（要素）を質問により気付かせます。次にその条件（要素）をどのように導くかを質問します。生徒は質問に答えながら自らの内に解を形成していくわけです。質問の連続により、生徒側からすれば質問に答える作業の連続により、生徒の自己回路に「生徒と教師」が解答の図柄を協働で描くわけです。「協働」といっても教師は「気づき」へのサポートを行うだけです。しかもその「気づき」も、サポートなしで気ずく必然性があるものを教師が顕在化させているだけなのです。
生徒の側は解への教師の図柄を（多くの場合）描けてはいません。教師の質問に答えながら、知らず知らずの内に、その図柄を自己の回路に沿った形に変容させながら、自らの内に描いていくわけです。そして図柄を描き終わった時、生徒は「一人でもこの図柄は描けたんだ」と意識することになるわけです。具体的事例を見てみます。
（実況中継）

「上図において△ＡＢＣの面積を求めよ」
Ａ「新人教師」　Ｂ「生徒」　Ｃ「研修指導教師」
Ａ「じゃーいくよ。…条件 は確認したよ。条件は全て図の中に書き入れるんだったね。△ＡＢＣの面積を出したいんだよね。
Ｂ君どうする？」
Ｂ「……」
Ａ「三角形の面積は底辺×高さ÷２だよね。じゃ底辺と…」
Ｃ「ちょっと待ってください。先生がその公式を言った瞬間に生徒がその公式を
覚えているかどうか、忘れているとすれば他の公式との混同か、全く忘れているのか等の情報を探る機会を失うことになりますね。もし他の公式との混同であれば、そのまちがえた方の公式の確認も必要になりますよね。教えると言うことは　生徒の回路の外に解を描くことになる可能性がありますよね。」
Ａ「じゃ三角形の面積の公式は？」
Ｂ「底辺×高さ÷２」
Ａ「いいね。じゃー底辺と高さをだそうか。ＢＣはどうやってだす？」
Ｃ「底辺はＢＣとは限りませんよね。サラッとでもいいですからＡＢ、などの斜めの長さをだすのは現在（中２）はできない事、又高さをだすこともできないことを説明する必要があります。」
Ａ「底辺はどこ？高さはどこ？前に来て指で示してごらん。」
Ｂ（正解を実行）
Ａ「そうだね。ただ底辺は三つの辺のうち下にあるものという規則があるわけではないので、どこの辺を底辺にしてもいいんだったね。（以下説明省略）じゃー君の指した底辺のBCをだして」
B「・・・」
Ａ「Ｂの座標はどうやってだす？」
Ｃ「先生はＢ君がどこでつまづいていると考えているんですか？」
Ａ「うーん多分、Ｂ,Ｃの座標のだし方」
Ｃ「今の段階では沈黙の原因は確定できないですよね。本当はわかっていて、自信がないから口にしない場合もありますし、BCの長さということとB,Cの座標を求めるということが結びついていない可能性もありますよね。勿論これまで何度もいうように“どこがわからないの？”は特殊なケース以外使わないんでしたよね。BCの長さに注目するところまでは来たわけですから、そのBCをだすには何が必要ですかという形で質問すればよいと思います。現在の立ち位置を明確にするだけで、次の課題がはっきりみえてくる場合があります。その立ち位置を雲をはらって明確に示すことは生徒を外的に誘導することではなく、生徒の自らの歩みをサポートする触媒機能となります。」
A「じゃーB君、底辺のBCをだすには何が必要？」
B「BとCの座標」
A「いいね。じゃーだして」
C「いいんですけど、指示はB点かC点か一つにしぼりこんだ指示が必要ですね。この場合はB,Cどちらでもいいと考えておられると思いますが順序が問題になる場合もありますよね。いずれにしても教師は日常的に質問が多義的にならないように気をつける習慣をつけた方が良いと思います。質問の意味が複数解釈できる時、生徒は内容以前に質問はどちらの意味なんだろうという位置でエネルギーと時間を使うことになります。」
A「じゃーBの座標をだして」
B「……」
A「私からC先生に質問です。この場面でBのy座標がゼロということをこちらから提示する方法以外に思いつかないんですけど、生徒からそれを引きだす方法はありますか？」
C「ありますね。B点の座標がだしにくいのは見かけ上x、y両方の座標がでてないからですよね。ｘ座標又はy座標の一方の数値が与えられていて、もう一方を求める問題は数多くやってきているわけですね。ですからその既知内容と同じだということを示して、生徒の既知の回路との接続をすればいいわけです。ちょっと私がやってみますね。」
C「B君今B座標を出したいんだよね。座標のだし方はこれまでもやっているんだよね。ｘ＝１の時yはどうやってだす？」
B「ｙ＝ｘ＋１のｘに１を入れる」
《これができなければ、その子は一定の本格的復習が必要ということになります。現在扱っている文章題は直線の式を求める力のあることを前提にした問題です。一方の値がでている時にもう一方の値が求められないということは、直線の式の求め方ができていないということで、この子にとってこの問題は不適であり、復習を優先するべきであるという判断がつきます》
C「いいね。ｙ＝５の時のｘの値は？」
B「ｙ＝ｘ＋１のｙに５を入れる」
C「いいね。つまり座標のうち一方が数字がわかっていれば、もう一方も式を利用して求められるんだよね。Bの座標も一方はでていないともう一方はだせないんだよね。 つまりｘとｙのうち一方はでているはずなんだよね。ｘ,ｙ一方の座標がみえた？」
B「……」
C「じゃーｙ座標は？」
B「ゼロ」
《ここで答えがでなければ座標イメージの復習ということになる》
C「じゃｘ座標だして」
B「０＝ｘ＋１…ｘ＝－１」
C「いいね。じゃーBの座標は？<ここで教師が引きとって（－１,０）といってはいけない。>」
B「（ー１,０）」
C「ではB（－１,０）,C（３,０）とでたところから再開して下さい」
A「BCの長さはどうなる？」
B「４」
A[ここで底辺は４とでました。]
C「ここは切り返しが絶対必要ですね。つまり正解がでた場合の理由やプロセスをきく作業です。全く同種の問題の場合は３回目,４回目はきかないこともありますが、少なくとも最初の１～２回は切り返しが必要ですね。問題を扱う以上単なる答え合わせでは意味がないわけで、授業内容の定着が目的であるはずです。ですから正答の場合でもそのプロセスや理由が重要なわけです。特に正解の場合、その理由説明をすぐに教師の方でやってしまう場合が多いようです。教師の方で結果が正しければプロセスも正しいにちがいないという思いこみがあるわけです。しかし正答した生徒にとっても、プロセスや理由を説明することで自己の回路を対象化（自分の外にだして自分がながめる）でき刻印が深くなります。特にここでは重要ポイント（長さの出し方）を復習するきっかけづくりのためにもプロセスを問うことが有効ですね。」
Ａ「もどってみます。Ｂ君ＢＣ＝４はどうやってだした？」
Ｂ「ＢとＣの座標を使いました」
Ｃ「細かいようですけど先程言いましたように発問は生徒の答え方が拡散（いろいろな答え方ができる）しないように言葉を選ぶべきです。今の場合Ｂ先生の『どうやってだした？』ではＡ君のように「Ｂ,Ｃの座標を使いました」のような答も可能なわけです。Ｂ先生は“３－(－１)”を確認したいんでしょう？」
Ａ「そうです」
Ｃ「ではどうきいたらいいですか。」
Ａ［式を質問します」
Ｃ「やってください。」
Ａ「Ｂ君、ＢＣ＝４はどうやってだした？式を言って」
Ｂ「右に３、左に１だから長さは４」
Ａ「はい、いいですね。式でいうと３－(－１)＝３＋１＝４ですね。」
Ｃ［それはまずいですね。Ｂ君の考え方と先生の式は少なくとも別物ですよね。」
Ａ［どちらでもよいのではないかと思うんですが］
Ｃ［座標が文字の場合Ｂ君の考え方ではうまくいきませんね。符号がわからないわけですから。座標が文字で長さがでていて、方程式にもっていく問題はたくさんありますよね。ですからＢ君の考え方を認めて、この場合はその考えかたが使えるが、文字の場合は差をとる考え方でないと長さが表せないことを説明して、最終的には適用範囲の広い、差で長さを求める方法を優先させるべきですね。」
<Ａ先生のＢ君への説明省略>
Ａ［ＢＣは４とでたね。次に何が必要？］
Ｃ「教師が高さといわないのはいいですね。底辺がでたから、次は高さに注目するのは当然と考えるのは教師の側の論理で、生徒は底辺などの部分を求めることに意識が集中し、大きな構想、大きな流れを意識できなくなっていることはよくあることです。全体（Ａ）→部分（Ｂ）→部分（Ｂ）の既知となった全体（Ａ’）→Ａ’の要請する部分（Ｂ’）→Ａ”……の流れとなりますから、ここではＡ’のレベルに生徒を立たせる必要があるわけです」
Ｂ「高さ」
Ａ［高さってどこ、前にでてきて書き入れてみて」
Ｂ「はい。」
<正解>
Ａ［いいですね。じゃー高さをだすには何がわかればいいの」
Ｂ［Ａの座標」
Ａ「どうやってだす？」
Ｂ「連立方程式をとく」
<以下省略>
以上の流れは次のようになっています。問題設定明示（三角形の面積）
→面積求める公式→公式を使うために必要な要素（底辺,高さ）の確認→要素をだす（座標をだす）。ここではX軸との交点の座標を求めるのに、既習内容と同じ土俵に引き入れて（ｘ,ｙ一つわかればもう一方がでる）既存回路をフルに活用する。
この流れでは教師が新たに付加したものはありません。教師が生徒の回路の内にあるものを顕在化させただけです。Ａ君は最後に「なーんだ。自分だけでもとけたじゃん」とつぶやくわけです。教師はここでは黒子であり、優れた黒子は表舞台に足跡を残さないものです。

（２）「教師の出番はココ！」
問答法では教師は黒子に徹するわけですが、勿論教師の固有の役割もあるわけです。整理をすると次のようになると思います。

a 授業内容を系統的に理解する。
b :新内容の量的確定とイメージ化（右脳的処理）、「ｺｺﾀﾞｹ」というしぼりこみを行ない「授業知」をつくる。(問答法)
c：新内容説明後は生徒の固有の回路に沿った解への歩みを生徒に歩ませるサポートを行う。
ｄ：生徒が正答した場合や、答の理由を述べた場合に、それを引きとって「わかりやすく、ポイント、核心」として再構成する事。

Ｖ「問答法の意義」

（1）「生徒の情報駆使能力を鍛える」
問答法は教師の回路ではなく、生徒の自己回路を授業の中心におく授業方法です。従来の多くの授業のように、教師が自分の回路に従って教え、生徒はそれを受け取る構図の授業では、生徒の主要な関心は、教師から一方的に与えられたものを“覚える”ということに向かざるを得ません。しかし教師が解を与えず、質問の連続により生徒自身に気づかせる問答法においては、生徒は質問に答える形で自ら考えて正解への道を歩まなければなりません。そこでは自らの持つ既習内容や経験知、勘をフルに動員させることに主要な関心が向くことになります。問題の解は教師にとっては既知のものであっても生徒にとっては未知のものです。問題解決に自分の回路をﾌﾙ動員する訓練は、問題解決能力や、情報駆使能力、広義の創造力、発想力の育成機能と密接に結びつくことになります。
（2）「生徒は結論ではなくプロセスを重視するようになる！」
生徒は答を与えられのではなく、自ら答への道を歩まなければ答は得られません。つまり答はプロセスの結果であり、しかるべきプロセスがあれば結果はついてくるものです。したがって、生徒は結果ではなくﾌﾟﾛｾｽを最も重視するようになります。

（3）「生徒を助手席ではなく、運転席に座らせることで定着率は飛躍的に高まる！」
道順を覚える最も効果的方法は自ら運転することです。助手席で３回乗るより１回運転した方が道は覚えられるものです。理由は脳科学の面からも論じられるでしょうが、はっきりしていることは当事者（運転している人）にとっては、道の選び方について情報管理が途切れない“線”として存在していることです。一方非当事者（助手席の人）にとっては重要な目印などを意識的に覚えたとしても、それは断続的な点としての情報とならざるを得ないということです。
即ち前者（運転している人）は目的地に到着するために必要なすべての情報（意識的、半意識的、無意識的）を管理しているののに対して、後者（助手席の人）は意識化された情報のみを対象とすることになります。しかも運転行為そのものと結びついてのみ得られる情報もあるわけです。
要するに自らプロセスを歩むことは、十回もまわりから説明されるよりはるかに定着率が高くなるということです。教師の一方的授業では、生徒は教師の回路に自分を適合させなければなりません。ここに多くの「落ちこぼし」を生む最大の原因があります。問答法においては授業内容が「生徒自身の回路（＝自己回路）」にくみこまれますから、生徒自身で答へのプロセスを再構築できる可能性は飛躍的に高まるわけです。
先にも触れましたように、生徒が教師に手を引かれて答へのプロセスを歩んだのでは、後で自分一人で歩く事は困難となります。一方、問答法では、右へ曲がるか、左へ曲がるかの判断を、曲がり角ごとに生徒自身から引き出すことになりますので、生徒が自ら１人で正解への道を歩くことのできる可能性は飛躍的高まることになります。

（4）「教師は生徒の生の状況に関心を向けざるを得ない」
教師の一方的授業においては、教師は生徒の状況を予測の範囲内で考慮すればよいことになります。即ち「できる限り」でよいわけであり、基準があるわけではありません。その面での手抜きも可能であることになります。又生徒のつまずき方は文字通り無限であり、あらかじめ想定することは不可能です。問答法授業においては、答は生徒から引き出さなければならず、教師が答を与えるのは失敗授業ということになります。そして引き出すための拠り所は生徒の内にある既知のもの（既習事項、経験知、etc）ですから、教師は生徒の現状に本格的に関心を向けざるを得ません。例えば、既習内容を拠り所にして答を導こうとした時、当然定着していると考えていた既習内容を生徒が理解していないことがわかれば、新範囲説明よりも本格的復習が先という判断もできることになります。

問答法の意義
・ 生徒がプロセスに関心を持つ
・ 情報駆使能力が鍛えられる
・ 自から歩むことで定着率が高まる
・ 教師は生徒の生の状況に関心を持つ

小田　清